Going back to my last post, our fancy balance proclaims that it weighs objects from 0 to 200 g with a precision of 0.001 g (that's one milligram). And it does – put an object on and the balance gives you an attractive-looking number on its prominent display reading 184.139 g, or something similar. It is precise to 1 milligram. It's not reading 184.138 g, neither is it reading 184.140 g, it is reading 184.139 g.
So does that mean our test object has a mass of 184.139 g? Unfortunately not. Just because the balance gives us that number that precisely, it doesn't mean that it is that accurate. University lecturers always have a good giggle when some poor unsuspecting first year student records an answer to a wildly inappropriate number of significant figures – for example she might measure a speed in the lab of 1.48392348837 m/s. Precise, yes. Accurate, no. However, when a third year student does the same time (I've usually got the message across by then, aided by deducting marks on assignments for stupid use of significant figures), the humour turns into despair.
So what does our test object weigh? (What is it's mass? I mean). Well, I can weigh it several times and see how the results are spread. I've done that. It's a few milligrams. On taking the object off, and putting it on again, I don't see the recorded mass change by more than three of four milligrams. If I take a lot of measurements, and work out the mean mass and its standard uncertainty (with a bit of statistics) I can get something that has a random uncertainty of only a milligram or so.
However, that still doesn't mean our test object has a mass of 184.139 g (or whatever our calculation says). I may have accounted for random uncertainty, by weighing it multiple times, but there's certainly other systematic sources of uncertainty. These are significant. Just look at the graph. This is the mass of the test object (as recorded by the balance) over the period starting Tuesday morning this week. Our object is getting lighter! Quite a lot lighter, too. It's moved about 40 mg over three days! That's about one part in 5000.
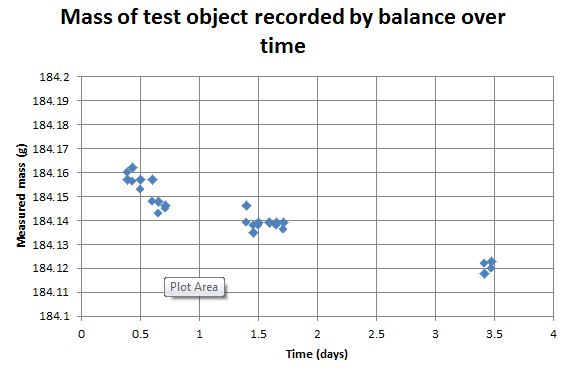
What's happening? One interesting thing to note is that we initially calibrated the balance with a nominal 200.000 g mass (sent with the equipment) and a completely empty pan (0.000 g). I've also been weighing the calibration mass and the empty pan over the course of the three days too. They have shown no drift at all – just a couple of milligrams of random uncertainty, as far as I can see.
The manual suggests that the equipment is affected by temperature and humidity. Now, Monday was one of those horrible Waikato days with a warm, damp atmosphere and lots of rain. One of those days where, if the humidity got any higher, it would be raining in your office. And there was a lot of rain Monday night, before I made the measurements. On Tuesday morning, everything 'felt' damp – but we've been drying out ever since. Is it a long-term drop in humidity in the lab that's caused the change? And is it because the test object was actually heavier (maybe there was some condensation on it) or is it because the humidity has made the balance 'stick' or affected the electronics in some way. I'm not sure?
But what I am sure about is that saying I have a 184.139 g test mass is, at present, unjustified.