If you drive an electric car more than trivial distances between charges, you likely appreciate a state-of-charge meter (that is, what would be called a fuel-gauge in a petrol car) that is accurate. When it reports a range of 30 km, you do want to be sure it will actually do this distance. If you run out of fuel in a petrol car, you can get a lift to the nearest petrol station, fill up a can of petrol, return to your car and get going again. With an electric car you need towing.
But there are numerous problems. How quickly your battery discharges will clearly depend on how you drive the car. An estimate of range will make some assumptions about how you are driving, and in what kind of conditions. That’s true in a petrol car too. Better might be to look at the ‘charge remaining’ indicator. (The picture shows a Nissan Leaf dashboard).

But that has problems too. It’s actually a really hard problem to work out how much charge is left in a battery. (I think this question is better framed in terms of ‘how much energy is left in a battery’ but I won’t dwell on that point.) My mobile phone is a good example. Despite (or maybe because of) having put it through a zillion charging cycles, the meter is still unbelievably useless at giving me a decent sense of how long it’s got left. If I charge it overnight it will start at 100% but rapidly fall to about 40% over the next few hours (even if I don’t use it for anything) and then start crawling downwards. After a couple more days of very limited use it might reach 2%, whereupon it will sit at that value for an indeterminate amount of time (I’ve had over a day out of it at 2%) until it decides to shutdown.
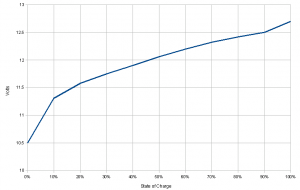
So how do you find out how much energy is left in a battery? There are several approaches to the problem. First, one might simply measure the battery voltage. As the stored energy reduces, the voltage reduces too. However, except at near 100% charge and 0% charge, the voltage on many types of batteries doesn’t change much with energy. That means that voltage isn’t a particularly sensitive measure of the remaining energy. A small uncertainty in the voltage translates to a large uncertainty in the energy. The graph below show the case for a lead-acid battery Between 80% and 70% charge, the voltage only drops by about 0.1 V, meaning small changes are hard to measure accurately. Once the voltage begins to drop quickly, you are already in trouble.
Another approach is ‘coulomb counting’. A coulomb is a unit of electric charge. By measuring the current drawn from the battery, one can integrate it with time (find the area under the current against time graph) to find the total charge that has been drawn. Since measuring current is reasonably straightforward and accurate, this approach is reasonable.
One can also carry out impedance spectroscopy – by measuring the changes in voltage for small changes in current at different frequencies we can get a measure of the charge in the battery. Impedance monitoring can also give a good measure of the state-of-health of the battery – i.e. when it’s about to fail.
However, even coulomb-counting has some conceptual difficulties. That’s because a battery doesn’t act purely as a charge storage device. Batteries have a resistive part to them, meaning that not all the energy you put in when charging will be recovered. Some energy is lost to heat. The same is true for supercapacitors. Normally, we’d expect capacitors to simply store charge, but supercapacitors are, in practice, not quite like capacitors. They obey fractional calculus. In a pure capacitor, the rate of change of voltage is just proportional to the current through them. So, for example, if you draw out a constant current, the voltage over the capacitor drops at a constant rate. But in a supercapacitor, the rate of change of voltage is not quite proportional to the current. Mathematically, the n-th derivative of voltage, where n is not quite 1 (maybe about 0.98 in practice) is what is proportional to current.
Fractional derivatives are a bit of a handful in calculus but the maths exists and they appear to describe supercapacitor and battery behaviour pretty well. But conceptually they carry a sting in the tail – the state of charge now becomes a function of not just the voltage now, but depends on the entire history of the voltage. That is, just measuring the voltage of a fractional element isn’t going to tell you the charge or energy left in it. We are going to need to know the entire history of the voltage to work it out. That point alone means making a battery-meter that actually works a very hard problem indeed.
