It’s that time of year when school students become seriously focused on exams. This year has been messy for student learning, and has affected some students more than others, but the NCEA external assessments and the Scholarship exams are going ahead pretty-much as normal.
I’ve taken some interest in the Scholarship Physics exams over the past years. It’s an exam that’s intended to flush out the very best physics-thinkers in the country, and award them appropriately. A student who does well at scholarship physics is one who doesn’t just know physics, but can ‘think’ physics. They can recognize physics principles and apply them in unfamiliar situations and talk critically about what they are doing. In other words, a student who gets Scholarship Physics is demonstrating what a real physicist does. And that’s why I like the exam.
The level of difficulty of questions tends to range from ‘hard’ through to ‘downright evil’. They can pull in multiple concepts and require many different steps in producing an answer. Having just perused a couple of recent scholarship exam papers, a couple of questions have left me gazing out of the window wondering how I’m going to start. But with some thinking – e.g. asking myself “what topic(s) is this question about?”, “what do I know about the physics in this problem?”, “what principles are going to apply here”, etc., I reckon I can tackle all questions.
Here’s an example from 2017:
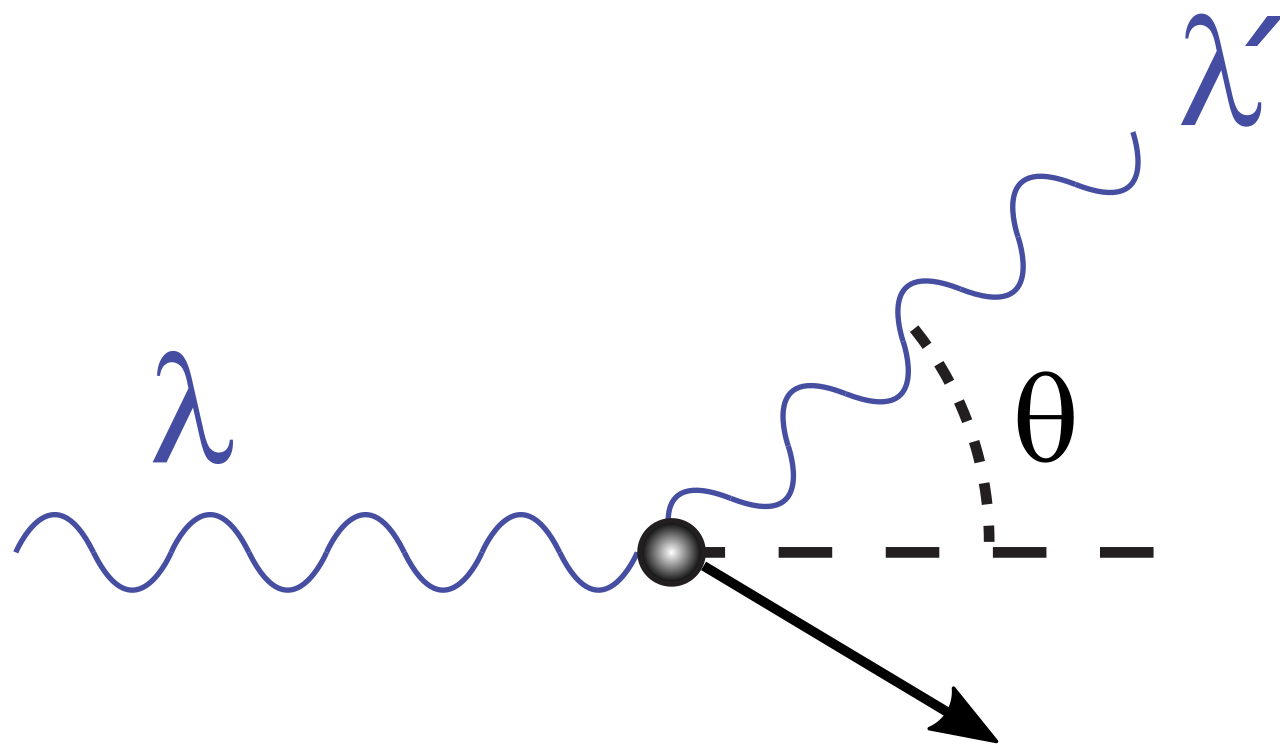
A photon of frequency f1 and wavelength lambda1, is scattered by a stationary electron. The photon has a momentum, given by the de Broglie relationship, of h/lambda1. Due to the interaction, a photon of frequency f2 and wavelength lambda2 results. It travels in the opposite direction to the initial photon, and the electron gains energy of 4.00 keV, with velocity v in the same direction as the incident photon. Calculate the value of lambda1. The effects of special relativity can be assumed to be negligible.
What is being talked about here is something known as ‘Compton Scattering‘, although you don’t need to know the name in order to tackle the question. A photon recoils elastically after a collision with a (near-)stationary electron. As a result the wavelength (or frequency, if you prefer) of the photon changes. Specifically, the wavelength increases, because the recoiling electron takes some energy from the photon.
If you’re preparing to do Scholarship Physics this year, you should have a go at this question. Once you’ve got it, or got completely stuck, read on…
I won’t give a worked answer for this, because there’s already one for you to look up with the documentation on the NZQA Scholarship website, including the ‘top scholar’s’ effort. (And if you’re preparing for the exam you should absolutely read this documentation since it tells you what successful students are doing well.) But, to produce an answer, a student is going to need to do the following:
- Apply conservation of momentum, including using the de Broglie relationship (given in the question) for momentum of a photon
- Apply conservation of energy, including recalling E=hf for the photon energy
- Relate the kinetic energy of an electron to its momentum, using K=p^2/2m
- Solve a simultaneous equation
- Convert an energy in keV to an energy in J
That is a lot of steps! It shows the challenge of the exam. Just knowing some equations isn’t going to get you through. You need to recognize the physics of what’s happening and apply the relationships, correctly. The exam paper provided 10 lines to write the answer, and I’d be impressed if you could squash your working into that space.
We used to have an experimental set-up in our third year physics lab that allowed students to do the Compton Scattering experiment. We used a gamma source (Cs-137) to provide the photons, and a copper rod as a source of ‘stationary’ electrons. Students then measured the wavelength shift of scattered photons with a spectrophotometer and analyzed how it varied with the angle of scatter. (In the scholarship question, the specific case of a scatter angle of 180 degrees – the photon comes back in the exact opposite direction- is considered, but in practice scattering happens at a range of angles. In fact, 180 degrees is the least likely case!)
Now, there’s a lovely relationship between the angle of recoil and the change in wavelength of the photon:
Change in wavelength = (h/mc) (1 – cos theta)
where h is Planck’s constant, m is the mass of the electron, c is the speed of light and theta is the angle of scatter (180 degrees for backscatter, as in the question.) Knowing the relationship wouldn’t help do this question, because we aren’t given either the initial or the final wavelength.
Interestingly, this equation is derived using special relativity. It should still apply at the low energies of this question (if you are really enthusiastic you can check this). Also, the equation requires consideration of both wave and particle natures of the incoming radiation – the former as a wavelength, the latter in terms of momentum and energy of photons. Overall, Compton Scattering captures a wide range of Modern Physics principles, making it a perfect candidate for a Scholarship Physics question. Arthur Compton was awarded a Nobel Prize in 1927 for his numerical analysis of the effect.
There is one thing about the question I don’t like, and that is that it’s rather contrived. In practice, this isn’t how Compton Scattering is experienced. To start with, complete backscatter is uncommon. Photons are far more likely to be scattered through small angles than large ones. Of course, there needs to be this special case considered in the question to avoid it becoming very hard indeed. Also, Compton Scattering is usually experienced at relativistic energies. The Cs-137 gamma ray which we used in the lab is at 662 keV, which certainly requires consideration of special relativity since it is above the rest mass energy of an electron of 511 keV. And finally, in practice, we don’t measure the kinetic energy of the electron – it’s inside a copper rod – how does one measure that? In practice, one relates the wavelength shift (which is measurable) to the angle of scatter (also measurable).
You still want to do Scholarship Physics? Get yourself prepared, and go for it.